梳理摄像头行人追踪经典论文SIMPLE ONLINE AND REALTIME TRACKING WITH A DEEP ASSOCIATION METRIC中的方法。

Simple online and realtime tracking with a deep association metric

作者：Nicolai Wojke, Alex Bewley, Dietrich Paulus

Abstract

Simple Online and Realtime Tracking (SORT) is a pragmatic approach to multiple object tracking with a focus on simple, effective algorithms. In this paper, we integrate appearance information to improve the performance of SORT. Due to this extension we are able to track objects through longer periods of occlusions, effectively reducing the number of identity switches. In spirit of the original framework we place much of the computational complexity into an offline pre-training stage where we learn a deep association metric on a largescale person re-identification dataset. During online application, we establish measurement-to-track associations using nearest neighbor queries in visual appearance space. Experimental evaluation shows that our extensions reduce the number of identity switches by 45%, achieving overall competitive performance at high frame rates.

1. 训练阶段

1.1 数据来源

使用 MARS 数据集：1.1 M 图像，1261 名行人，跨相机跨时段。
训练集/验证集拆分：按身份划成 631/630 两组用于训练和验证，保证 ID 不重叠。
增广：水平翻转、随机擦除、颜色扰动、256×128 LetterBox。

1.2 网络结构

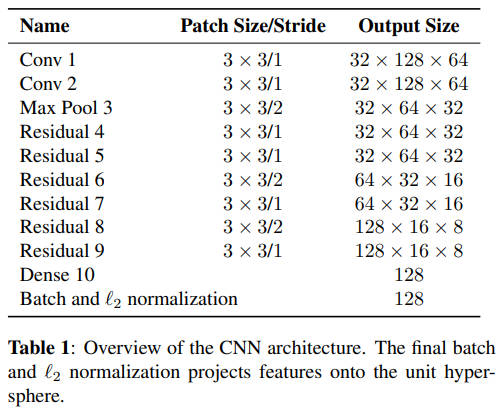
输入 (3,256,128) 的图像

Conv1 3×3/1 32 通道
Conv2 3×3/1 32 通道
MaxPool 3×3/2
6 个残差块（通道 32→64→128，下采样 2 次）
GAP（全局平均池化） (128,8,4) → 128 维向量
Dense10 128-D
BatchNorm1d + L2 归一化 → 单位球面输出

1.3 损失与训练协议

batch-hard 三元组损失的核心思想是，在一个 mini-batch 里，只留最难的样本去推/拉网络，忽略其余轻松样本，避免梯度被大量简单对淹没。batch-hard的 batch 构造过程如下

先随机抽 P=18 个行人身份（可以理解为 18 个人）
对每个人，再从不同相机、不同帧里各抓 4 张图，共 18×4=72 张图

对任意一张锚图：

找出同身份里外观最不像锚的那张图（同身份中余弦距离最大），作为最难正样本
找出异身份里外观最像锚的那张图（同身份中余弦距离最小），作为最难负样本

只保留这一对难样本计算损失，其余全部忽略。损失函数引用了文章 Simple online and realtime tracking with a deep association metric 中的计算方法。

损失函数：

\mathcal{L}_{\mathrm{BH}}(\theta; X) = \sum_{i=1}^{P} \sum_{a=1}^{K} \left[ m + \max_{\substack{p=1,\dots,K \\ p \neq a}} D(f_\theta(x_a^i), f_\theta(x_p^i)) - \min_{\substack{j=1,\dots,P \\ j \neq i}} D(f_\theta(x_a^i), f_\theta(x_n^j)) \right]_+

其中：
$P$ ：batch 中身份（person）数量
$K$ ：每个身份的图像数
$x_a^i$ ：第 $i$ 个身份的第 $a$ 张图像（anchor）
$x_p^i$ ：与 anchor 同身份的最远正样本（hardest positive）
$x_n^j$ ：与 anchor 异身份的最近负样本（hardest negative）
$D(·,·)$ ：欧氏距离（作者明确使用非平方欧氏距离）
$m$ ：margin，取 0.2
$[·]_+$ ：ReLU，即 $max(0, ·)$

我们来拆解一下这个公式。

外层双重求和
$\sum_{i=1}^{P} \sum_{a=1}^{K}$
一次 mini-batch 里有 $P$ 个身份，每人 $K$ 张图；对每张图 $(i,a)$ 都当一次锚点，共 $P×K$ 个锚点。
最难正样本项
$\max_{\substack{p=1,\dots,K \\ p \neq a}} D(f_\theta(x_a^i), f_\theta(x_p^i))$
在同身份 $i$ 的其余 $K-1$ 张图里，找距离最大的那张作为硬正样本（hardest positive）。作用是把同身份最远的点拉进来，防止簇内松散。
最难负样本项
$\min_{\substack{j=1,\dots,P \\ j \neq i}} D(f_\theta(x_a^i), f_\theta(x_n^j))$
在所有异身份图里，找距离最小的那张作为硬负样本（hardest negative）。作用是把最迷惑人的异类推远，增大类间 margin。
Hinge项
$[m + (hardest positive) − (hardest negative)]_+$
当 $hardest positive$ 比 $hardest negative$ 远（或近得不够）时， hinge 项为正，损失产生梯度，否则为 0，损失为 0。

训练协议：

优化器：Adam
学习率：0.0001
mini-batch：72
epoch：1000
保存频率：每 100 个 epoch 保存一次

2. 识别流程

2.1 输入检测

检测器给出 (u,v,w,h) + 置信；置信 <0.3 的直接丢弃。该文章的检测器来自于Poi: Multiple object tracking with high performance detection and appearance feature，是一个Faster R-CNN 在私有+公开行人数据集上重新训练的一个强检测器。

2.2 特征提取

框图等比缩放到 256×128，侧补灰条；
每个通道减去 ImageNet 均值 $μ$ ，再除以标准差 $σ$ ，即 $x = (x_raw / 255.0 - μ) / σ$ ；
前向冻结 CNN → 128-D → L2 归一化 → 单位向量 $r_j$ 。把 RGB 图像压成 128 维单位超球面向量

2.3 运动预测与门控

目标：在下一帧到来之前，用“常速模型”估计每个轨迹的新位置，并给出一个置信椭圆——只有检测框落在这个椭圆内，才允许参与后续匹配。整个流程分为三步：状态定义 → 预测 → Mahalanobis 门控。

状态向量与观测
采用图像平面上的 8 维常速模型。
状态 $x = [u, v, γ, h, u̇, v̇, γ̇, ḣ]ᵀ$
– $(u,v)$ ：框中心像素坐标
– $γ = w/h$ ：宽高比
– $h$ ：高度像素
– 带点项为对应一阶导数（速度）

1.2 观测 $z = [u, v, γ, h]ᵀ$

预测阶段
对已存在轨迹 $k$ ：
用上帧估计 $(x̂_{k-1}, P_{k-1})$ 做先验预测

x̂_k|k-1 = F x̂_{k-1|k-1}

P_k|k-1 = F P_{k-1|k-1} Fᵀ + Q

其中 $F$ 为状态转移矩阵， $Q$ 为过程噪声协方差矩阵。
预测输出
均值 $y_i = H x̂_k|k-1$ → 4-D 框 $(u,v,γ,h)$
协方差 $S_i = H P_k|k-1 Hᵀ + R$

门控阶段
对新检测框 $d_j = (u_j, v_j, γ_j, h_j)$ ，计算到预测分布的平方 Mahalanobis 距离：

d^(1)(i,j) = (d_j - y_i)ᵀ S_i^{-1} (d_j - y_i)

4-D 观测空间下，平方 Mahalanobis 距离服从 $χ²$ 分布，获取95 % 置信区域对应的阈值 $t_{95}$ ，若 $d^(1)(i,j) < t_{95}$ 则认为通过门控，允许进入匈牙利成本矩阵。

2.4 外观匹配与门控

目的：把程度低的配对直接踢掉，减少匈牙利矩阵的歧义，同时让轨迹在遮挡后靠外貌重新找回身份。
循环画廊（Circular Gallery）
每条轨迹 k 维护一个固定长度 100 的列表 $R_k = [r^(1), …, r^(100)]$ ，元素是 128-D 单位向量（L2 归一化后），来自过去 100 次成功匹配的检测特征。每成功匹配一次，把新特征 push 进队尾，超出 100 则 pop 队头
最小余弦距离计算
对新检测 $j$ ，先提取 128-D 单位向量 $r_j$ ，然后与画廊逐向量求余弦相似度

sim(l) = r_j^T r_k^(l) ∈ [-1, 1]

d^{(2)}(i,j) = min_l { 1 - sim(l) } ∈ [0, 2]

取最小距离, 即最像的那个历史向量。
3. 硬门控（Hard Gating）

b^{(2)}_{i,j}=\begin{cases}1,&d^{(2)}(i,j)\leq0.2\\0,&\text{otherwise}\end{cases}

2.5 成本矩阵与级联

两轮门控（运动 + 外观）都通过后，该 (轨迹 $i$ , 检测 $j$ ) 对才被允许进入匈牙利算法的成本矩阵。接下来顺序如下：

构造成本矩阵 C
仅保留 $b^{(1)}=1$ 且 $b^{(2)}=1$ 的配对
元素 $C_{i,j}$ = 外观余弦距离
未通过门控的位置填 $∞$ ，确保匈牙利不会选中
匈牙利最优分配
在 $C$ 上求解最小成本匹配
输出：最优 (轨迹→检测) 列表 + 未匹配轨迹 + 未匹配检测
Kalman 更新 / 新建轨迹 / 删除轨迹
匹配成功的：用对应检测框做 Kalman 更新，并把其 128-D 特征压入轨迹 gallery
未匹配检测：初始化暂定轨迹，需连续 3 帧成功关联才转正
未匹配轨迹：age +1，超过 $T_{lost}$ （默认 30）帧即删除
循环结束：下一帧到来时，用更新后的轨迹状态回到第 1 步预测阶段。

Tianyao' s BLOG

DeepSort (SIMPLE ONLINE AND REALTIME TRACKING WITH A DEEP ASSOCIATION METRIC)