本文简单介绍了GIS空间分析/地统计中极其基础，但非常重要的算法：核密度分析
核密度估计法认为地理事件可以发生在空间的任何位置上，但是不同的位置上事件发生的概率不一样。点密集的区域事件发生的概率高，点稀疏的地方事件发生的概率低，核密度估计即获得随机变量在每个可能取值处出现的概率。
根据概率理论（Rosenblatt-Parzen核估计），核密度估计的定义为：
其中，$X1,……Xn$为从分布密度函数为f的总体中抽取的样本，$f_n (x)$是估计函数f在某点x处的值。$K()$称为核函数，h为带宽，$(x-Xi)$表示估值点x到事件Xi处的距离。
核函数的选择对统计结果有很大的影响。常用的核函数主要为经典核函数，高斯核函数、四次多项式函数等。其中，高斯核函数的公式为：
读者可以发现，所谓高斯核函数，其实就是高斯分布概率函数的变换，相比高斯概率密度函数：
核密度函数将标准差$\sigma$ 换成了带宽$h$，将$x-\mu$(均值)换成了$x - x_i$（核密度估计函数里的高斯核函数，自变量为$x - x_i$）。实际上，就是将高斯函数作为加权工具。让我们回到一开始描述的核密度估计的目的：获得随机变量在每个可能取值处出现的概率，剖析一下这一问题。
1970年，地理学家威廉·托布勒（William Tobler）提出了著名的地理学第一定律：
“Everything is related to everything else, but near things are more related than distant things.”
翻译过来的就是“一切事物都与其他事物相关，但接近的事物比远离的事物更相关。”这条定律的核心思想是：地理空间上距离越近的地方，它们之间的相互作用和相似性就越高，距离越远的地方则相互作用和相似性就越低。这意味着地理空间上的事物不是孤立的存在，而是相互联系、相互作用的。
譬如你的唯二两个邻居李二王五都身家千万，那么地理学家会估计你也是个富哥。继续增加条件，李二身家1000万，他家距离你家2km，王五身家2000万，他家距离你家3km，那么地理学家可以将你的身家推算为：(1000x2+2000x3)/(2+3)=1600万，这就是地理学中著名的反距离权重插值：
现在你了解了地理学中空间连续的思想，再回头重新理解核密度函数，其概念可以被解释为：用区域内事件的多少，来估计该地发生事件的概率。并且，越靠近该位置的地方发生的事件，必然对该位置是否发生事件的影响更大，这大小体现在权重上，因此上述高斯核函数，就是对传统的反距离加权的补充，相比反距离函数，高斯函数在概率上更加贴合现实情况。
为演示，我使用海南省两个仙级行政区人口分布数据做了简单的核密度分析。图中，sigma即带宽h。
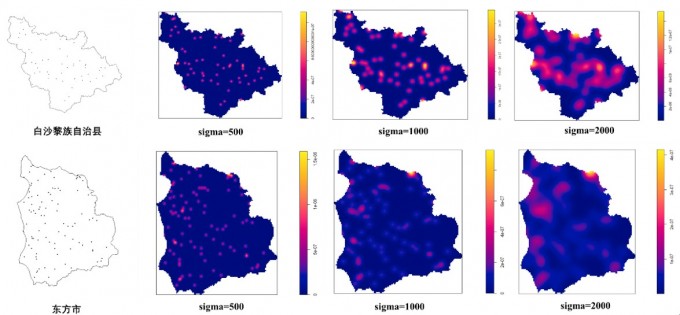
可以清晰的看到，随着内核直径sigma的增加，核密度估计的影响范围也沿着点像四周扩散。每个数据点对密度估计的贡献范围就越大，产生更加粗略的密度图像。
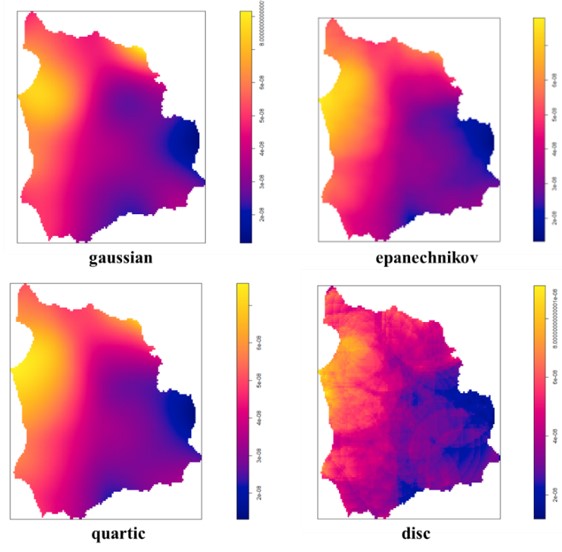
高斯核函数（Gaussian kernel）具有平滑的形状，能够很好地把每个数据点的影响扩散到周围的区域。高斯核函数的带宽与核宽度是同一个概念，均等于核函数的标准差（sigma）。
经典核函数（epanechnikov kernel）具有类似三角形的形状，在距离较近的区域有较大的权重，而在距离较远的区域权重减小。经典核函数的带宽等于核函数的最大值，即 2。核宽度则等于带宽的一半，即 1。
四次多项式函数（quartic kernel）具有类似方形的形状，在距离较近的区域有较大的权重，而在距离较远的区域权重减小。四次多项式函数的带宽和核宽度由使用者定义。
圆锥函数（disc kernel）具有类似圆锥形的形状，在距离较近的区域有较大的权重，而在距离较远的区域权重减小。圆锥函数的带宽（bandwidth）等于核函数的最大值，即 2。核宽度（kernel width）则等于带宽的一半，即 1。
在图中可以看到，前三种插值方式得出的结果较为相似，都相对平滑，但是圆锥核函数插值得出的结果则较为粗糙，且数据间过渡不平滑。